AMD MI60 벤치마크
Posted: 2025-04-20 / Last Modified: 2025-04-23
AMD MI60 사양
Radeon Instinct MI60은 AMD가 2018년 11월 18일에 출시한 전문가용 그래픽 카드다. 이 카드는 7nm 공정으로 제작되었으며, Vega 20 GL 버전의 Vega 20 GPU를 기반으로 한다. DirectX 12를 지원한다.
Vega 20 GPU는 다이 면적 331 mm², 총 132억 3천만 개의 트랜지스터로 구성된 대형 칩이다.
자세한 사양과 이론적 성능은 다음과 같다. (출처: TechPowedUp)
| 항목 | 내용 |
|---|---|
| 출시일 | 2018년 11월 18일 |
| GPU 아키텍처 | Vega 20 (Vega 20 GL) |
| 공정 기술 | 7nm |
| 트랜지스터 수 | 13,230백만 (13.23억) |
| 기본 클럭 | 1200 MHz |
| 부스트 클럭 | 최대 1800 MHz |
| 메모리 용량 | 32 GB HBM2 |
| 메모리 인터페이스 | 4096-bit |
| 메모리 속도 | 1000 MHz |
| 인터페이스 | PCI-Express 4.0 x16 |
| 최대 소비 전력 | 300W |
설치 서버 및 비교 대상 서버
elgin
| 항목 | 상세내용 |
|---|---|
| CPU | 2 x Intel(R) Xeon(R) Silver 4110 |
| GPU | 2 x AMD Instinct MI60 |
| Compiler | llvm-amdgpu@6.3.3 + rocm-openmp-extras@6.3.3 |
| Compile option | -O3 -fopenmp -fopenmp-targets=amdgcn-amd-amdhsa -Xopenmp-target=amdgcn-amd-amdhsa -march=gfx906 |
AMD Instinct MI60 이론성능 수치
| 이론 성능 항목 | 성능 수치 |
|---|---|
| 픽셀 처리율 (Pixel Rate) | 115.2 GPixel/s |
| 텍스처 처리율 (Texture Rate) | 460.8 GTexel/s |
| FP16 (반정밀도) | 29.49 TFLOPS (2:1) |
| FP32 (단정밀도) | 14.75 TFLOPS |
| FP64 (배정밀도) | 7.373 TFLOPS (1:2) |
gwave
| 항목 | 상세내용 |
|---|---|
| CPU | 2 x Intel(R) Xeon(R) Gold 6530 |
| GPU | 2 x NVIDIA GeForce RTX 4090 |
| Compiler | nvhpc@25.3 |
| Compile option | -O3 -mp=gpu |
NVIDIA GeForce RTX 4090 이론성능 수치
| 이론 성능 항목 | 수치 |
|---|---|
| 픽셀 처리율 (Pixel Rate) | 443.5 GPixel/s |
| 텍스처 처리율 (Texture Rate) | 1,290 GTexel/s |
| FP16 (반정밀도) | 82.58 TFLOPS (1:1) |
| FP32 (단정밀도) | 82.58 TFLOPS |
| FP64 (배정밀도) | 1,290 GFLOPS (1:64) |
gmunu
| 항목 | 상세내용 |
|---|---|
| CPU | 2 x AMD EPYC 7702 |
| GPU | GPU 없음 |
| Compiler | gcc@13.2.0 |
| Compile option | -O3 -fopenmp -march=znver2 -mtune=znver2 |
벤치마크 문제
블랙홀에 의한 시공간
\[ ds^2 = -\left(1-\frac{2}{r}\right)dt^2 +\left(1-\frac{2}{r}\right)^{-1}dr^2 +r^2d\theta^2+r^2\sin^2\theta d\phi^2 \tag{1} \]여기서 \(c=G=M=1\) 유닛을 사용하였고 sign convention은 \((-,+,+,+)\)이다. 하지만 이 좌표계를 바로 적용하면 \(\theta=0\) 근처로 빛이 지나갈 경우 정확하게 기술하기 어려워 진다. 그리고 앞으로 이 연구의 확정을 위해서는 직교좌표계를 도입하는 것이 매우 유리하다. 이를 위하여 슈바르츠실트 계량(metric)을 아래과 같은 좌표 변환을 하면 등방 좌표계(isotropic coordinates)로 표현할 수 있다.
\[ r=R\left(1+\frac{1}{2R}\right)^2 \label{eq:coord_trans}\tag{2} \]그리고 위 (식 \ref{eq:coord_trans}) 좌표 변환을 통한 등방 좌표계에서의 슈바르츠실트 메트릭은 다음과 같다.
\[ \begin{split} ds^2 &= -\frac{\left(1-\frac{1}{2R}\right)^2}{\left(1+\frac{1}{2R}\right)^2}{dt}^2 + \left(1+\frac{1}{2R}\right)^4\left(dR^2+R^2d\theta^2+R^2\sin^2\theta d\phi^2\right) \\ &= -\frac{\left(1-\frac{1}{2R}\right)^2}{\left(1+\frac{1}{2R}\right)^2}{dt}^2 + \left(1+\frac{1}{2R}\right)^4\left(dx^2+dy^2+dz^2\right) \end{split} \label{eq:metric_iso} \tag{3} \]여기서 \(R=\sqrt{x^2+y^2+z^2}\)이다.
빛의 궤적
\[ \frac{d^2 x^a}{d\lambda^2}+\Gamma^a_{bc}\frac{d x^b}{d\lambda}\frac{d x^c}{d\lambda} = 0 \label{eq:geodesic}\tag{4} \]여기서 \(\lambda\)는 Affine parameter으로 빛의 궤적을 파라미터 화 시킬 수 있다. 식 \ref{eq:geodesic}는 2계 전미분 방정식으로 초기 조건이 결정되면 미래(혹은 과거)의 위치와 속도를 모두 결정할 수 있는 초기값 문제(initial value problem)다.
상대론적 광선추적법을 이용한 블랙홀 주변 디스크 이미지
\[ R_{\rm{in}} = \frac{5+2\sqrt{6}}{2}, \quad R_{\rm{out}} = 70. \]여기서 \(R_{\rm{in}}\) 값은 ISCO(Innermost Stable Circular Orbit)의 크기이다. 디스크는 z축을 경계로 케플러 회전 속도로 회전 하는 것으로 가정하였다. 또한 디스크는 단 파장을 내는 디스크로 가정하였고 R이 커질수록 R^2에 비례해서 어두워지는 모델을 가정하였다.
관측자는 디스크 평면에서 \(5^{\circ}\) 각도를 이루고 있으며 블랙홀에서 \(1000M\) 떨어진 관측자로 설정하였고 관측자의 해상도는 2048x1024이고 스텝 사이즈(h)는 h=-0.005로 설정하였다 (총 ray의 갯수는 2,097,152개이고 디스크와 만나지 않는 ray의 경우 대략 460,000번 integration이 진행 됨).
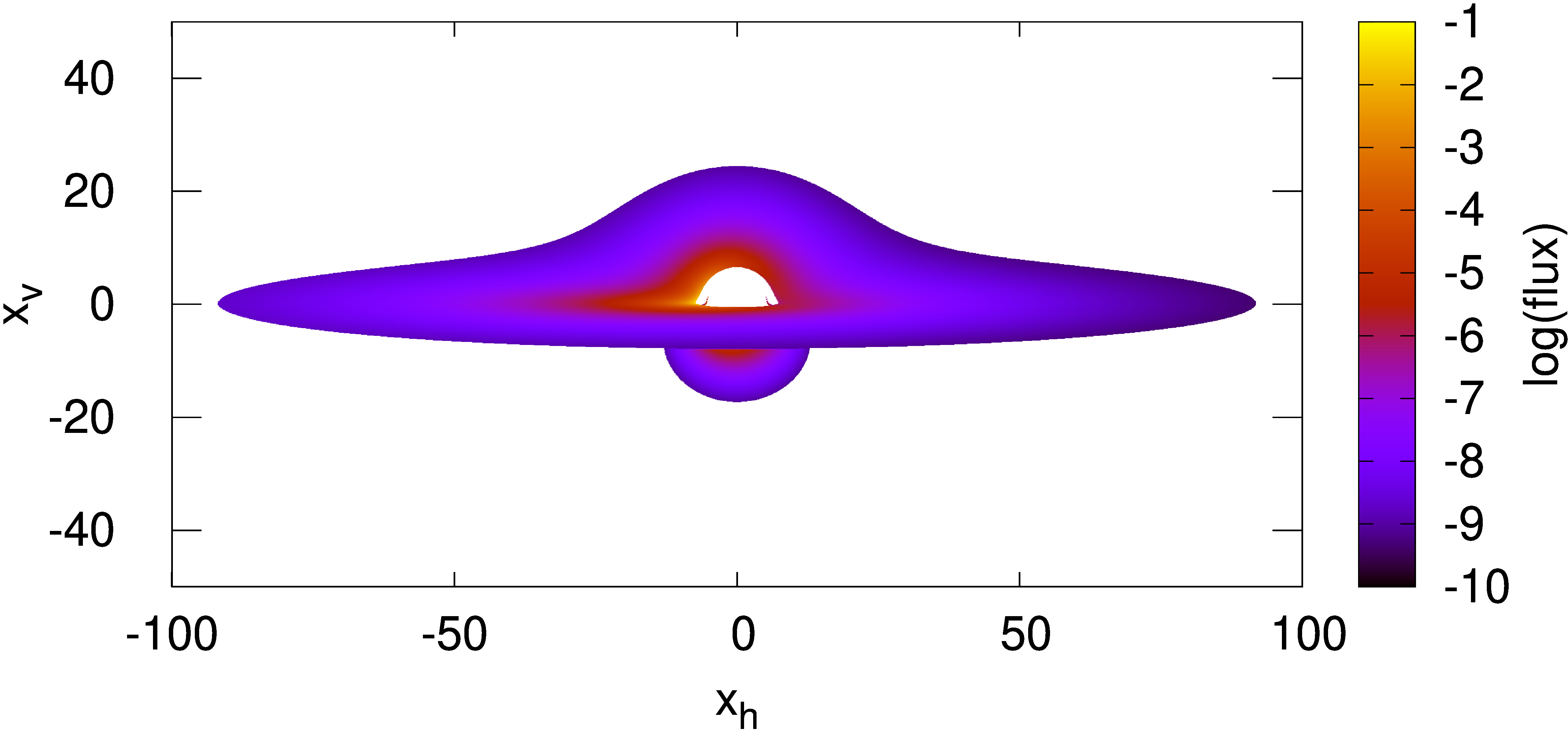
디스크의 플럭스가 강한 부분은 디스크의 회전에 의해서 청색편이가 일어난 부분이다.
벤치마크 결과
수치 코드는 OpenMP GPU offloading을 하였고 (OpenMP 4.0부터 지원) Multi-GPU 환경에서는 device 지정(OpenMP 5.0부터 지원)으로 GPU 갯수 만큼의 patch로 나누어서 계산하였다.
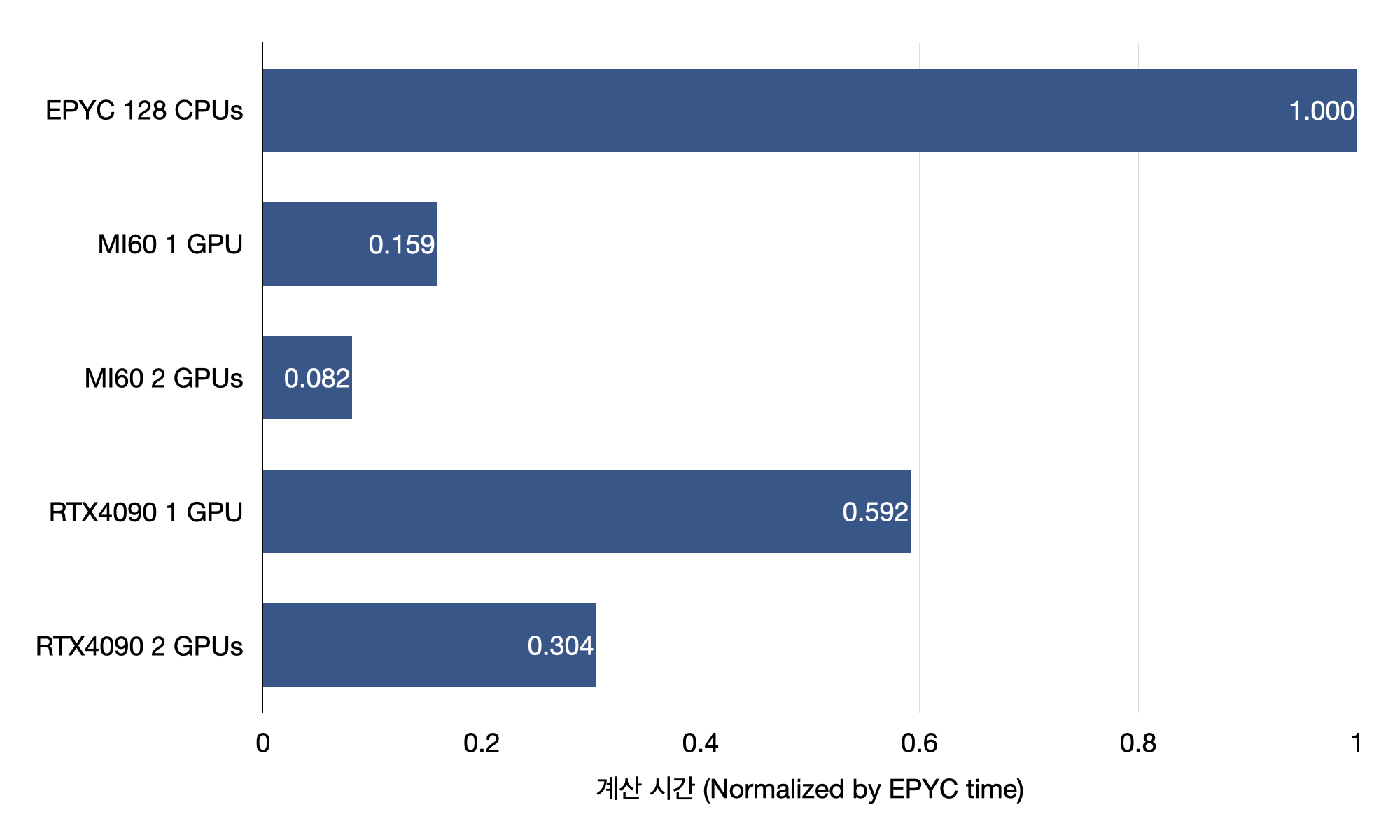
벤치마크 테스트 결과 이론적 성능과 같이 FP64 성능이 우수한 MI60가 높은 성능을 보여준다. 다만 MI60의 경우 llvm 컴파일러를 사용 (AMD 권장 컴파일러) 하였으나 NVIDIA컴파일러 대비 성능이 다소 떨어지는 결과를 보여주었다. 특히 RTX 4090의 경우 llvm 컴파일러를 사용할 경우 약 7%정도 성능 하락이 있었다.
이 결과는 각각의 그리드가 서로 데이터를 주고받지 않는 이상적인 계산이므로 실제 유체역학 등 PDE 계산에서는 성능이 다소 하락 할 것으로 예상 된다.